Let’s take a look at this A maths question on Equations and Inequalities. A handful of students will be confused with the keywords or how to effectively determine the correct sign of the discriminant.
The example below is very similar to St Margaret 2016 A Math Prelim Paper 1 Q2.
Original Question: Find the range of values of \(p\) for which \((p+2)x^2 – 12x + 2(p-1)\) is always negative.
Modified Example: Find the range of values of \(p\) for which \((p+2)x^2 – 12x > -2(p-1)\) for all real values of \(x\).
Misconception:
Students will mistaken REAL as the keyword and likely think that \(b^2-4ac \geq 0\).
The emphasis is that the word REAL is crucial ONLY if coupled with a friend called ROOTS. We need to see the Keyword – REAL ROOTS for \(b^2-4ac \geq 0\) to hold true.
Step 1:
Ensure that the right hand side of the inequality is zero.
\((p+2)x^2 -12x + 2(p-1) > 0\)Step 2:
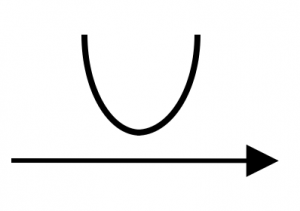
Having done so, recognise the keyword as “\(>0\)“. This implies that the graph will be above the axis and the shape of this quadratic expression will be a Happy Face. Since the U-shape is not intersecting with the axis, the solutions will be imaginary and \(b^2-4ac < 0\).
Keyword \(>0\) implies
\(\Rightarrow\) Happy Face is ABOVE axis
\(\Rightarrow\) No Real Solutions
\(\Rightarrow\) \(b^2-4ac < 0\)
Step 3:
Observe \(a=p+2, b=-12\) and \(c=2p-2\)
For imaginary solutions, we have :
\(b^2-4ac<0\)
\((-12)^2-4(p+2)(2p-2)<0\)
\(144-4(2p^2-2p+4p-4)<0\)
\(-8p^2-8p+160<0\)
\(-p^2-p+20<0\)
\((-p+4)(p+5)<0\)
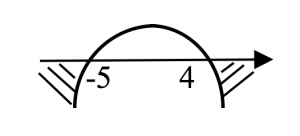
\(p<-5\) or \( p>4\)…..(1)
At this stage, most students are contented with getting the solutions and will think that the question is completed.
Well, we are almost there. This is a typical example of having a variable coefficient (\(p+2\)) in front of \(x^2\).
Extra Step is mandatory
Remember we mentioned earlier that the graph is a Happy Face, thus we expect the coefficient of \(x^2\) to be positive and we have
\(p+2>0\)
\(p>-2\)….. (2)
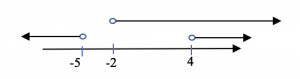
Visualise the overlapping region of answers on a number line from (1) and (2),
Therefore \(p>4\) (final solution)