JC2 Topical Revision – A Levels Preparation

Vectors

Lesson 1: 16 – 22 June 2025
Lesson 2: 23 – 29 June 2025

Lesson Focus:

• • Key Formulas and Definitions:  
    • • Ratio Theorem
      • Scalar (dot) product and vector (cross) product definitions and applications

• • Equations of Lines and Planes: Learn how to find and express the equations of lines and planes in various forms (vector, parametric, Cartesian).
  • Foot of Perpendicular: Find the foot of the perpendicular from a point to a line or a plane
  • Angles Between Vectors, Lines, and Planes: Calculate angles between two vectors, two lines, two planes, and between a line and a plane.
  • Distances in 3D Geometry:
    • From a point to a line or plane
    • Between skew lines
    • From the origin to a plane
    • Between parallel planes

• • Planes at a Given Distance: Derive equations of planes that lie a fixed distance away from a given plane.
  • Relationships Between Lines and Planes:
    • • Identify whether lines and planes are parallel, intersecting, or skew.
      • Analyze the geometric relationships using direction vectors and normal vectors.

• • Reflections in 3D: Reflect points, lines, and planes across other planes
  • Geometrical Interpretations: Understand the meaning of scalars and position vectors in geometric contexts.

Differentiation Applications

Lesson: 1 – 6 July 2025

Lesson Focus:

• • Tangent and Normal Lines:
    • • Solve problems involving the equations of tangents and normals to parametric curves.
      • Understand the geometric meaning and how to compute gradients using dy/dx​.

• • Converting Parametric to Cartesian Equations:
    • • Learn how to eliminate parameters to form Cartesian equations from parametric ones.
      • Tackle questions involving the complete curve traced by parametric equations.

• • Lines Parallel to the Axes: Apply properties of curves where parts are parallel to the x-axis or y-axis, and how this affects their derivatives.
  • Sketching Parametric Curves:
    • • Accurately sketch parametric curves by identifying key points (e.g., endpoints, intercepts, turning points) and direction of travel.
      • Recognize domain restrictions and behavior at boundaries.

• • Concavity of Curves: Determine concavity using second derivative and understand its interpretation in sketching.
  • Rate of Change Problems: Apply parametric differentiation to real-world rate of change questions involving related variables.
  • Maximum and Minimum Problems: Use derivatives to identify turning points on parametric curves and solve optimization problems involving max/min values.

Maclaurin Series

Lesson: 7 – 13 July 2025

Lesson Focus:

• • Forming the Maclaurin Series:
    • • Learn how to manipulate given functions and apply the Maclaurin series formula.
      • Understand when and how to expand standard functions.

• • “Hence” Questions Using Known Series:
    Tackle typical “hence” question types:
    • • Using binomial expansion
      • Differentiating or integrating existing series to form new ones
      • Substituting or transforming the input to derive related series

• • Approximations and Error Analysis:
    • • Understand how to evaluate percentage error in approximation problems.
      • Provide qualitative assessments of whether a given series offers a good approximation within a range.

• • Range of Accuracy: Determine the range of x-values for which a Maclaurin series approximates the original function to within k units.
  • Small Angle Approximation: Apply small angle approximations in appropriate contexts
  • Linking Trigonometry and Series: Apply sine and cosine rules in problems, and explore how binomial expansions can relate to trigonometric approximations in modeling scenarios.

Sequences: APGP

Lesson: 14 – 20 July 2025

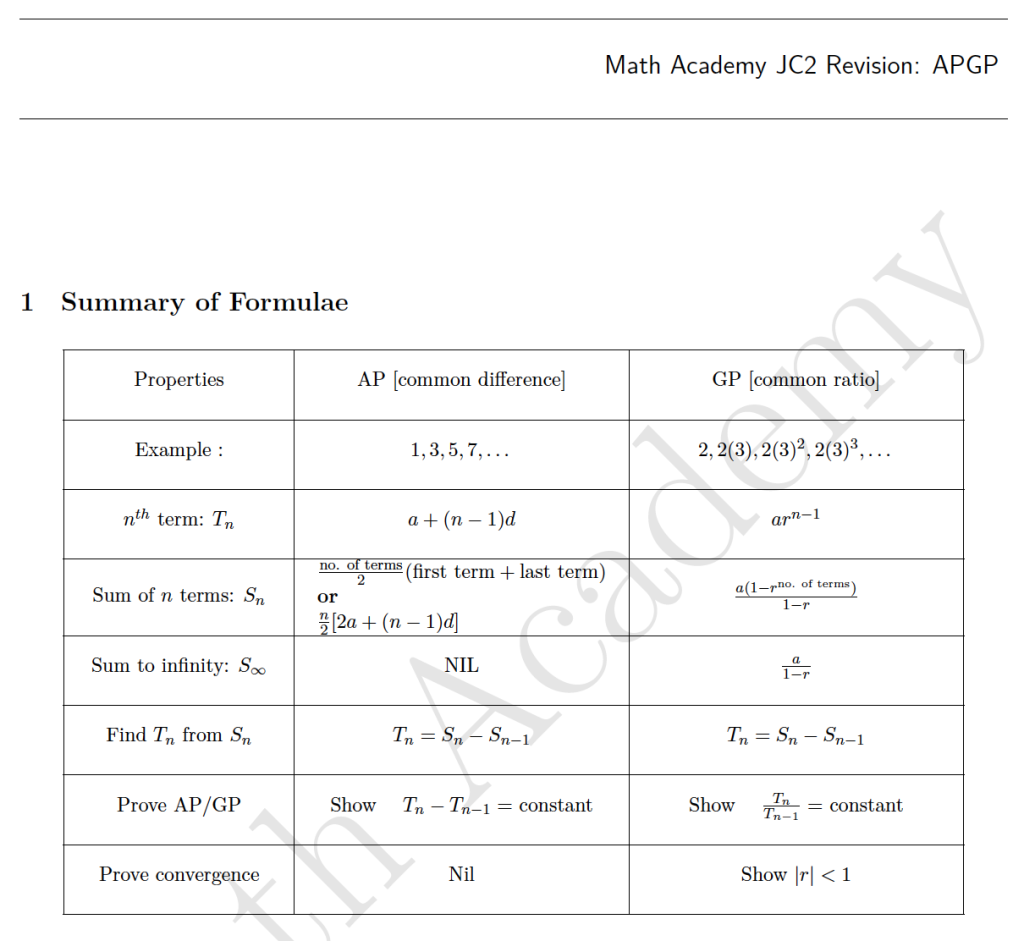
Lesson Focus:

• • Key Formulae Summary:
    • • General term of an arithmetic/geometric progression
      • Sum of the first n terms
      • Sum to infinity (for convergent GP only)

• • Proof and Convergence: Prove the formulas for AP and GP using algebraic techniques
  • Odd and Even Term Concepts:
    • • Identify and work with odd- and even-numbered terms in sequences
      • Apply these concepts to evaluate specific terms or patterns in a sequence

• • Conditional Sums: Calculate the sum of integers within a given range, subject to specific conditions (e.g. odd multiples of 3 from 1 to 100)

• • Consecutive Terms in GP:
    • • Understand the relationship between consecutive terms in a geometric progression
      • Use these relationships to form and solve equations involving unknowns

• • Contextual and Real-World Applications: Solve contextual problems, especially in financial settings (e.g. compound interest, depreciation, savings plans) using AP/GP models

Sequences: Recurrence

Lesson: 21 – 27 July 2025

Lesson Focus:

• • Solving Sequences Using Simultaneous Equations: Apply simultaneous equations to find unknowns in both arithmetic and geometric sequences.
  • AP and GP in Summation: Use arithmetic and geometric progression formulas to evaluate sums and solve related problems.
  • Recurrence Relations: Learn how to solve for unknowns in recurrence relations and interpret their structure.
  • Graphing Calculator (GC) Applications:
    • • Use the GC to find specific terms in a sequence efficiently.
      • Explore sequence behavior visually and numerically using the GC, and learn how to present solutions accurately.

• • Limits and Convergence of Sequences:
    • • Solve for the limit of a sequence and justify convergence.
      • Prove whether a sequence is increasing or decreasing within a given range using three different methods

• • Identifying a GP in Recurrence Relations: Learn how to recognize and prove that a recurrence relation forms a geometric progression.

Summation of Series

Lesson: 28 July – 3 Aug 2025

Lesson Focus:

• • Properties of Sigma Notation: Understand key properties of summation and how they can be used to simplify or manipulate expressions.
  • Expanding Summations: Learn how to apply these properties to “open up” or break down a sum into simpler components.
  • AP and GP Summations: Identify arithmetic and geometric progressions within sigma notation and apply the appropriate sum formulas.
  • “Hence” Replacement Questions: Tackle common exam-style questions involving general terms and changing upper/lower limits—understand how to manage shifts in index values.
  • Using Graphing Calculator (GC): Learn how to use the GC effectively to solve for unknown integer values

Integration Techniques

Lesson: 4 – 10 Aug 2025

Lesson Focus:

• • Summary of Key Formulae: Review essential integration formulas commonly used in exams.
  • Application to Exam Question Types: Learn how to apply integration techniques to frequently tested question formats.
  • Fractions with Quadratic Denominators: Master techniques for integrating rational functions—know when to factorise or complete the square, and how to proceed with integration accordingly.
  • Trigonometric Integration: Tackle integrals involving trigonometric functions, including handling powers and factoring techniques.
  • Substitution and Integration by Parts: Understand when and how to apply substitution and integration by parts effectively.
  • Modulus Integration: Learn how to split the integral based on modulus expressions, determine the correct limits, and assign appropriate signs for each section.

Applications of Integration

Lesson: 11 – 17 Aug 2025

Lesson Focus:

• • Area with Respect to the x- or y-Axis: Learn how to calculate the area under a curve using integration along the x- or y-axis.
  • Area Between Two Curves: Understand how to find the area of the region bounded between two curves, including when and why a negative sign is necessary.
  • Volume of Revolution (x- and y-Axis): Identify scenarios where the graph needs to be divided (“cut up”) before applying the volume of revolution formula.
  • Single vs. Dual Curve Rotation: Recognize when to rotate a single curve around an axis, and when to find the volume between two curves by applying the “outer minus inner” method.
  • Area Under a Curve Using Limits of Sums: Learn how to estimate area under a curve using the limit of a sum of rectangles — including identifying correct rectangle height, distinguishing between overestimation and underestimation, and applying limits to arrive at the exact area.

Differential Equation

Lesson: 18 – 24 Aug 2025

Lesson Focus:

• • Integration: Identify common types of integration problems frequently tested in exams and learn how to apply the correct techniques and formulas effectively.
  • Substitution Methods: Understand and tackle various substitution-based integration questions.
  • Differential Equations (Contextual Problems): Learn how to form the correct differential equations from real-world contexts, with emphasis on commonly tested exam formats.
  • Graph Sketching in Differential Equations: Review exam-style problems and key pointers on interpreting and sketching solution curves accurately.

Functions

Lesson: 25 – 31 Aug 2025

Lesson Focus:

• • Properties of 1-1 Functions:
    • • Understand the concept of a one-to-one (1-1) function.
      • Show that a function is 1-1 by using the horizontal line test.

• • Inverse Functions:
    • • Understand the properties of inverse functions, including the relationship between their domains and ranges.
      • Learn how to find inverse functions, especially for quadratic equations
      • Understand how to decide on the correct sign for the square root in different scenarios.
      • Use completing the square or the quadratic formula 

• • Composite Functions:
    • • Understand the properties of composite functions
      • Find the domain of the composite function.
      • Determine when a composite function exists.
      • Use the mapping method to find the range of a composite function.

• • Relationship Between a Function and Its Inverse: Explore the relationship between a function f f-inverse and its inverse f-inverse f.
  • Graphing Functions and Their Inverses:
    • • Learn how to graph on the same diagram and what to look out for.
      • Use a graphing calculator (GC) to sketch the inverse function without explicitly solving for its equation.

• • Piecewise Functions and Compositions: Solve for equations of new composite functions involving piecewise functions.

Graphing Techniques

Lesson: 1 – 7 Sept 2025

Lesson Focus:

• • Sketching Rational Graphs: Learn how to identify and sketch rational functions, focusing on determining the equations of asymptotes (both vertical and horizontal).
  • Range of Values for Rational Graphs: Solve algebraic problems involving the range of values a rational graph can take, including understanding domain restrictions and behavior at asymptotes.
  • Stationary Points and Discriminants: Apply the discriminant to find the number of stationary points on a graph.
  • Conics:
    • • Understand the key properties of conic sections (ellipse, hyperbola, and parabola) through their general equations.
      • Be able to sketch these conic graphs manually (without GC), identifying key features such as vertices, and centre, to deepen conceptual understanding.

• • Partial Conics: Sketch only a portion of the graph (half or specific sections) based on the context and requirements of the problem.
  • Conic Transformations and Applications: Solve typical exam “hence” problems involving transformations of conics, such as stretching an ellipse or modifying a circle, and understand the impact of these transformations on the graph.

Transformation of Graph

Lesson: 8 – 14 Sept 2025

Lesson Focus:

• • Understanding Transformations:
    • • Learn the relationship between different transformations (translation, scaling, reflection) and their corresponding replacements in equations.
      • Understand how changes in the equation affect the graph
      • Translation (shifting)
      • Scaling (stretching/compressing)
      • Reflection (flipping)

• • Solving Examination Problems:
    • • Work through typical examination problems to gain exposure to the variety of transformation-related questions.
      • Focus on forming equations based on the description of transformations, both for direct transformations (given an equation, apply the transformation) and reverse transformations (given the transformed equation, deduce the original).

• • Modulus Graphs:
    • • Learn how to draw modulus graphs accurately, and understand the order of transformations (e.g., reflecting, translating, and scaling) in relation to modulus functions.

• • Reciprocal and Derivative Graphs:
    • • Understand the properties of reciprocal graphs and their derivatives.
      • Learn how to graph these accurately, paying attention to key features like asymptotes and intercepts.

• • Recovering the Original Graph:
    • • Learn how to recover the original function y=f(x) from transformed graphs like y=f(∣x∣) or y=f′(x).
      • Understand the effect of absolute value and differentiation on the graph’s shape and characteristics.
    •  

Inequalities

Lesson: 15 – 21 Sept 2025

Lesson Focus:

• • Inequalities on the Number Line: Solve algebraic inequalities by expressing solution sets using number line diagrams.
  • Always Positive/Negative Expressions: Learn how to determine when an expression is always positive or negative.
  • Modulus Inequalities: Learn how to ‘open up’ modulus signs
  • “Hence” Question Types (General Forms): Tackle exam-style “hence” questions that involve replacing variables with common functions (e.g., x^2, e^x, ln x etc).
  • “Hence” Questions Involving Trigonometry: Construct the trigo graph to solve for the inequality
  • Using Graphs and Graphing Calculators (GC):
    • • Learn to solve inequalities by interpreting intersections and shaded regions on graphs.
      • Use GC effectively to visualize and verify solution sets.
    •  

Permutation and Combination

Lesson: 22 – 28 Sept 2025

Lesson Focus:

• • Codeword Problems: Techniques for forming codewords using a subset of letters from a given word, including how to systematically break the problem down into manageable cases based on length, letter choice, and order relevance.
  • Passcode Problems (Digits & Letters): Solving passcode-related questions involving digits and/or letters, with emphasis on whether repetition is allowed, order matters, and how to handle constraints like “must contain at least one digit”.
  • Distribution Problems: Strategies for distributing identical or distinct objects into groups. Includes approaches for both distinguishable and indistinguishable groups, and when to use permutations vs. combinations.
  • “At Least” Questions: Methods to handle questions involving “at least” or “at most” conditions, including the complement method and structured case-by-case breakdowns for clarity and accuracy in exams.
  • Separation of Items into Sets: Understanding the difference between separating one set of items (e.g., ensuring no two are adjacent) and separating two distinct sets, a concept that has been tested in past A-Level papers.
  • Circular Permutations & Rotational Symmetry: Solving problems involving circular arrangements and symmetry.

Probability

Lesson: 29 Sept – 5 Oct 2025

Lesson Focus:

• • Venn Diagram Problems: Learn how to solve question types involving Venn diagrams, with a few key formula to apply and remember.
  • Minimum and Maximum Value Problems: A common exam-style question: finding the minimum or maximum possible value in a venn diagram under given conditions. These will be approached using a clear, step-by-step method to ensure accuracy and completeness.
  • Tree Diagram Questions: Understand how to construct and analyze tree diagrams for probability problems, especially those involving dependent or conditional events. Emphasis will be placed on probability paths and total probability.
  • Permutation and Combination Applications: Master how to recognize and apply permutation and combination techniques within exam questions. Focus will be given to translating word problems into structured counting strategies.
  • Geometric Progression in Probability: Identify and solve problems involving geometric progressions in probability contexts—especially those requiring summing infinite series to calculate total probability.

Discrete Random Variable

Lesson: 6 – 12 Oct 2025

Lesson Focus:

• • Summary of Expectation and Variance Formulas: A concise review of key formulas used to calculate the expectation (mean) and variance of discrete random variables, including linear transformations and functions of variables.
  • Constructing Outcome Tables: Learn to identify when it’s necessary to build a complete table of all possible outcomes—usually for questions involving the sum or product of two events, such as rolling two dice.
  • Solving ‘Fairness’ Questions: Understand how to approach problems involving fair games or scenarios, where expected values are used to determine conditions for fairness.
  • Case Listing for Independent Observations: Practice listing all possible outcomes for independent observations of a given variable, and learn how to calculate the combined distribution or total expected value.
  • Application of the Central Limit Theorem (CLT): Apply the Central Limit Theorem to solve probability questions involving the sum or average of discrete random variables, and understand how the normal approximation is used in such contexts.

Binomial Distribution

Lesson: 13 – 19 Oct 2025

Lesson Focus:

• • Key Properties of the Binomial Distribution: Understand the three essential properties that define a binomial distribution. Focus will be placed on exam-style questions that ask for the assumptions required to model a variable as binomial. The class will include the exact phrasing needed to secure full marks in written responses.
  • Identifying Trials and Successes: Techniques and tips to help students clearly identify what constitutes a single trial and a success, especially in less straightforward problem setups.
  • Common Problem Type: “k-th Success is the n-th Trial”: Explore a frequently tested question type where the k-th occurrence of a success happens on the n-th trial, and learn how to model and solve these using the appropriate binomial reasoning.
  • Finding the Mode of a Binomial Distribution Using the GC: Learn how to use the graphing calculator to determine the mode of a binomial distribution efficiently, including the interpretation of output.
  • Using Central Limit Theorem (CLT) with Binomial Variables: Apply the CLT to approximate probabilities for binomial variables when n is large, using the normal distribution as an approximation.
  • Relating Pk and Pk+1 Using the Binomial Formula: Use the binomial probability formula to establish and manipulate relationships between consecutive probabilities, a skill often required in proof-based or inequality-style questions.
  • Explaining and Using the Mode to Find a Range of Unknown Values: Understand how the mode of a binomial distribution can be used to find a range of unknown values—highlighted through a walkthrough of a past A-level exam problem.

Normal Distribution

Lesson: 20 – 26 Oct 2025

Lesson Focus:

• • Key Formulae and Properties of the Normal Distribution: Review the essential properties and formulas, including how they apply to linear transformations (e.g., aX+baX + baX+b) and to the sum/difference of two normal variables.
  • When to Apply Standardization: Learn to recognize scenarios where standardizing to the standard normal distribution Z∼N(0,1) is appropriate, and decide whether to use the graphing calculator (GC) graph vs tables, or manual calculations.
  • Finding the Mean and Average of a Normal Variable: Understand how to interpret and calculate the mean and expected value of normally distributed variables, especially in context-based questions involving sample averages.
  • Modulus-Type Questions: Tackle question types involving modulus expressions (e.g., ∣X−μ∣), especially when keywords like “differs by”, “within”, or “at most” are present. Learn how to spot these cues and translate them into probability statements.
  • Solving Inverse Normal (invNorm) Questions with Inequalities: Handle inverse normal distribution questions where the given probability is linked to an inequality (e.g., find the value of x such that P(X>x)<0.2).
  • Sketching Normal Distribution Curves
  • Learn to accurately draw normal distribution curves to reflect various conditions given in the question. Understand the 68-95-99.7 rule (empirical rule) and how to use the concept of three standard deviations to identify extreme values or check for reasonableness.
  • Cost and Percentage Change Questions: Solve normal distribution questions involving cost-related contexts, including scenarios with percentage increases or decreases. Focus on setting up the mean and standard deviation after adjustment.

Hypothesis Testing

Lesson: 27 Oct – 2 Nov 2025

Lesson Focus:

• • Correct Use of Symbols for Mean and Variance: Review how to accurately use symbols for the population mean (μ), sample mean (x̄), population variance (σ²), sample variance (s²), and unbiased estimates. Emphasis will be placed on choosing the correct notation based on context.
  • Using p-values and z-critical Values to Reject H0​: Understand how to compare the p-value with the significance level (α), and how to use z-critical values to determine whether to reject the null hypothesis in one-tailed or two-tailed tests.
  • 5 Key Steps in Hypothesis Testing: Learn the standard 5-step structure for presenting hypothesis tests in exams – students will be shown the exact phrasing and steps expected for full marks.
  • When to Apply the Central Limit Theorem (CLT): Recognize situations where the CLT must be quoted, especially when dealing with sample means from non-normal distributions but large sample sizes.
  • Identifying Keywords for Formulating H1: Learn how to spot keywords that indicate the correct form of the alternative hypothesis. Learn how to handle special keywords such as overstate, at most, etc
  • Key Definitions & Accurate Phrasing: Understand and memorize definitions of important terms like:
    • • Unbiased estimate
      • Significance level
      • p-value
      • Random sample
        Learn how to phrase definitions contextually to meet exam requirements.

• • Finding the Critical Region: Learn how to determine the critical region for hypothesis tests, and apply this to a past A-level exam question to reinforce understanding.